2016-S5 Circle of Life
Problem Description
View Problem
Key Insight #1
The circle of life problem requires you to study the relationships between the generations of cells. The first key insight is that the value of the cell in the next generation is the XOR of its neighbors. The problem paper describes it as “If exactly one of a cell’s neighbours is alive in the current generation, then the cell will be alive in the next generation. Otherwise, the cell will be dead in the next generation.” We can see that this can be represented by an XOR operation.
XOR Truth Table
| A | B | Result |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Brute Force Implementation
A brute force solution that receives 5/15 points and uses a bit shifting approach.
Key Insight #2
If we analyze the progression from generation to generation we can come to the following conclusion.
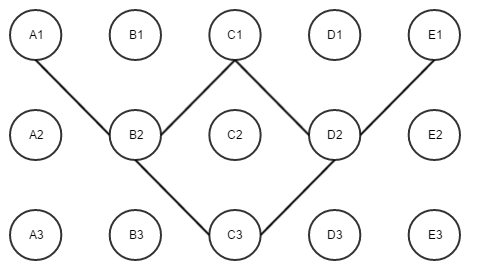
B2 = XOR( A1, C1 )
D2 = XOR( C1, E1 )
C3 = XOR( B2, D2 )
C3 = XOR( XOR( A1, C1 ), XOR( C1, E1 ) )
C3 = XOR( A1, E1 )
The magic is how we get to last statement. No matter what the value of C1 is C3 is always equal to the XOR of A1 and E1. We can show this using a quick truth table.
| A1 | C1 | E1 | XOR( XOR( A1, C1 ), XOR( C1, E1 ) ) | XOR( A1, E1 ) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
Using this formula we can skip a generation and calculate the end result more quickly.
Key Insight #3
We can generalize the formula above by saying that a cell N that is T generations old is equal to the XOR of its neighbors that are T cells away from it. This formula works as long as T is a power of two. With this in mind the solution is clear.
- We need to read in the initial configuration.
- We need to determine the largest power of two that is smaller that the number of generation we still need to simulate.
- Simulate that many generations.
- If we have finished we output the ending configuration otherwise we return to step two.
Please attempt to solve the problem on your own before viewing the solution!
View Solution